Pembahasan Soal UN Matematika SMP 2017 Paket 1

Soal UN Matematika SMP/Mts 2017 dan Pembahasannya._

Soal Nomor 1

Hasil dari $81^{3/4}$ adalah .......
A. $18$
B. $27$
C. $36$
D. $54$

Pembahasan Soal Nomor 1

Sifat eksponen yang digunakan:
$\bbox[yellow,13px] {(a^{m})^{n} = a^{m \times n}}$

Tips:
Untuk menyelesaikan soal di atas, pertama-tama kita ubah angka 81 ke dalam bentuk pangkat. Lalu setelah itu, gunakan sifat eksponen di atas untuk menyelesaikannya.

Penyelesaian :
$\begin{align} 81^{3/4} & = (3^{4})^{3/4} \\ & = 3^{3} \\ & = 27 \end{align}$


Jadi, Hasil dari $81^{3/4}$ adalah $27$


Jawab : B

Soal Nomor 2

Hasil dari $2\sqrt{27} \times \sqrt{32} : \sqrt{48}$ adalah .......
A. $3\sqrt{3}$
B. $4\sqrt{3}$
C. $5\sqrt{2}$
D. $6\sqrt{2}$

Pembahasan Soal Nomor 2

Tips:
Untuk menyelesaiakan soal di atas, pertama-tama kita ubah bilangan berbentuk akar $(\sqrt{27}, \sqrt{32}, \sqrt{48})$ ke bentuk sederhananya. Setelah itu, kita selesaikan soal di atas seperti biasanya.

Penyelesaian :
$\begin{align} \require{cancel} & \; \quad 2\sqrt{27} \times \sqrt{32} : \sqrt{48} \\ \\ & = {2\sqrt{9 \times 3} \times \sqrt{16 \times 2} \over \sqrt{16 \times 3}} \\ \\ & = {2 \times 3 \times \cancel{\color{red}{\sqrt{3}}} \times \bcancel{\color{red}{4}} \times \sqrt{2} \over \bcancel{\color{red}{4}} \times \cancel{\color{red}{\sqrt{3}}}}\\ \\ & = 6 \sqrt{2} \end{align}$


Jadi, Hasil dari dari $2\sqrt{27} \times \sqrt{32} : \sqrt{48}$ adalah $6 \sqrt{2}$


Jawab : D

Soal Nomor 3

Bentuk sederhana dari $\dfrac{8}{3-\sqrt{5}}$ adalah .......
A. $6 + 2\sqrt{5}$
B. $6 + \sqrt{10}$
C. $6 - \sqrt{10}$
D. $6 - 2\sqrt{5}$

Pembahasan Soal Nomor 3

Merasionalkan Pecahan Berbentuk Akar
$\bbox[yellow,13px] {\dfrac {a}{b-\sqrt{c}} = \dfrac {a}{b-\sqrt{c}} \times \dfrac {b+\sqrt{c}}{b+\sqrt{c}} = \dfrac {ab + a\sqrt{c} }{b^{2} - c}}$

Tips:
Kalikan penyebut dan pembilang pecahan berbentuk akar dengan bilangan bentuk sekawan penyebutnya. Karena penyebutnya berbentuk bil. $3-\sqrt{5}$, maka bilangan sekawannya adalah $3+\sqrt{5}$

Penyelesaian :
$\begin{align} \dfrac{8}{3-\sqrt{5}} & = \dfrac{8}{3-\sqrt{5}} \times \dfrac{3+\sqrt{5}}{3+\sqrt{5}} \\ \\ & = \dfrac{24 + 8\sqrt{5}}{9-5} \\ \\ & = \dfrac{24 + 8\sqrt{5}}{4} \\ \\ & = 6 + 2 \sqrt{5} \end{align}$


Jadi, Bentuk sederhana dari $\dfrac{8}{3-\sqrt{5}}$ adalah $6 + 2 \sqrt{5}$


Jawab : A

Soal Nomor 4

Perhatikan pola pada gambar berikut!

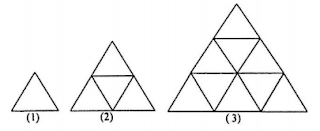
Banyak segitiga sama sisi dengan ukuran satuan pada pola ke-8 adalah .......
A. $81$
B. $72$
C. $68$
D. $64$

Pembahasan Soal Nomor 4

Gambar di atas membentuk pola bilangan $1,4,9,.......$
Jika diperhatikan, ternyata bilangan di atas membentuk pola barisan aritmetika.

Agar lebih mudah dalam menyelesaikan soal di atas, perhatikan gambar ilustrasi di bawah ini :

Barisan Aritmetika Tingkat 2


Cara Pertama :
Rumus Aritmetika Tingkat Dua :
$\bbox[yellow,13px] {U_{n}= a + \left (n-1\right)b+ \dfrac {\left (n-1\right)\left (n-2\right)c}{2}}$

Dik :
$a = 1 \\ b = 3 \\ c = 2$

Maka, Banyak segitiga pada pola ke-8 adalah
$\begin {align} \require{cancel} U_{n}& = a + \left(n-1 \right)b+ \dfrac {\left(n-1 \right)\left (n-2 \right)c}{2}\\ U_{8}& = 1 + \left(8-1 \right)3 + \dfrac {\left(8-1 \right)\left (8-2 \right)2}{2}\\ & = 1 + \left(7 \right)3 + \dfrac {\left(7 \times 6 \times \cancel{2} \right)}{\cancel{2}}\\ & = 1 + 21 + 42 \\ & = 64 \end {align}$



Cara Kedua :
$\bbox[yellow,13px] {U_{n} = a + \text{S}_{n-1}}$
Keterangan :
$a = $ Suku pertama barisan artimetika pertama
$\text{S}_{n-1} = $ Jumlah n suku pertama barisan aritemetika kedua


Dik :
Barisan Aritmetika pertama $=1, 4, 9$ dengan $a=1$
Barisan Aritmetika kedua $=3, 5, 7$ dengan $a = 3 \quad b = 2$


Penyelesaian :
$\begin{align} U_{n} & = a + \text{S}_{n-1} \\ U_{8} & = 1 + \text{S}_{8-1} \\ U_{8} & = 1 + \text{S}_{7} \\ & = 1 + \dfrac{n}{2} \left(2a + \left(n-1\right)b \right)\\ & = 1 + \dfrac{7}{2} \left(2.3 + \left(7-1\right)2 \right)\\ & = 1 + \dfrac{7}{2} \left(6 + 12 \right)\\ & = 1 + \dfrac{7}{2} \left(18 \right)\\ & = 1 + 63 \\ & = 64 \end{align}$


Maka, banyak segitiga pada pola 8 adalah $64$


Jawab : D

Soal Nomor 5

Suku ke-10 dari barisan bilangan : $15, 24, 35, 48. 63, ...$ adalah .......
A. $120$
B. $143$
C. $168$
D. $195$

Pembahasan Soal Nomor 5

Untuk menyelesaikan soal nomor 5, caranya hampir sama dengan nomor 4

Agar lebih mudah dalam menyelesaikan soal di atas, perhatikan gambar ilustrasi di bawah ini :

Barisan Aritmetika Tingkat 2 :


Penyelesaian :
Dik:
$a = 15 \\ b = 9 \\ c = 2$

Maka, suku ke-10 barisan bilangan tersebut adalah
$\begin {align} \require{cancel} U_{n}& = a + \left(n-1 \right)b+ \dfrac {\left(n-1 \right)\left (n-2 \right)c}{2}\\ U_{10}& = 15 + \left(10-1 \right)9 + \dfrac {\left(10-1 \right)\left (10-2 \right)2}{2}\\ & = 15 + \left(9 \right)9 + \dfrac {\left(9 \times 8 \times \cancel{2} \right)}{\cancel{2}}\\ & = 15 + 81 + 72 \\ & = 168 \end {align}$


Maka, banyak segitiga pada pola 8 adalah $168$


Jawab : C

Terima kasih